Pengujian Hipotesis Deskriptif Satu Sampel Statistik Parametris
Pengujian hipotesis deskriptif merupakan proses pengujian generalisasi hasil, yang hasilnya didapatkan dari satu buah sampel. Kesimpulan yang diperoleh dari hasil pengujian adalah keputusan berupa apakah hipotesis tersebut dapat digeneralisasikan atau tidak dapat digeneralisasikan hasilnya. Jika H0 diterima maka hasil hipotesis dapat digeneralisasikan, jika tidak maka hipotesis tidak dapat digeneralisasikan. Dalam proses pengujiannya, variabel penelitian yang digunakan adalah variabel yang bersifat mandiri. Oleh karena itu, hasil dari penelitian yang didapat tidak berupa perbandingan ataupun hubungan antar dua variabel atau lebih.
Sebelum mempelajari materi tentang Pengujian Hipotesis Deskriptif Satu Sampel Statistik Parametris, terlebih dahulu pelajari materi tentang: Rumusan Hipotesis Statistika dan Penjelasannya, Tingkat Kesalahan Pengujian Hipotesis Statistika Penelitian, dan Kesalahan Pengujian Hipotesis Statistika Penelitian.
Secara visual pengujian hipotesis deskriptif dapat diperlihatkan pada gambar 1. Terdapat beberapa macam teknik statistik yang dapat digunakan dalam proses pengujian hipotesis deskriptif. Dari semua teknik pengujian tersebut, teknik mana yang layak untuk dipakai adalah tergantung dari jenis data yang akan diamati atau dianalisis seperti diperlihatkan pada tabel 1.
Pada tabel 1 diperlihatkan hubungan antar jenis data terhadap data statistik yang digunakan, yaitu berupa statistik parametris dan nonparametris. Statistik parametris digunakan jika daya yang akan diamati berbentuk tipe data interval atau tipe data rasio. Sedangkan jika tipe datanya adalah tipe data nominal atau tipe data ordinal, maka yang dipergunakan adalah statistik nonparametris. Statistik parametris bekerja berdasarkan asumsi bahwa data yang akan dilakukan pengamatan adalah terdistribusi normal, sedangkan untuk jenis data yang terdistribusi secara bebas akan digunakan untuk statistik nonparametris. Bagi kedua jenis statistik, baik itu statistik parametris maupun statistik nonparametris, kedua jenis statistik tersebut selalu berasumsi bahwa data sampel yang akan digunakan sebagai sumber data adalah jenis data yang dapat diambil secara acak atau random.
Terdapat dua teknik pengujian hipotesis deskriptif dengan menggunakan satu buah sampel, yaitu teknik uji dua pihak atau two tail test dan teknik uji satu pihak atau one tail test. Teknik uji satu pihak juga dibagi lagi menjadi dua jenis yaitu, uji pihak kanan dan uji pihak kiri. Teknik uji mana yang kemudian dapat digunakan pada hipotesis adalah tergantung dari bentuk permasalahan atau pertanyaan yang diajukan dalam kegiatan penelitian.
Persamaan yang dapat digunakan dalam proses penghujian hipotesis deskriptif satu sampel yang menggunakan data sampel interval atau rasio diperlihatkan pada rumus 1 berikut.
Berikut adalah tahapan yang dilakukan untuk melakukan pengujian hipotesis deskriptif:
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
Selanjutnya, Uji Dua Pihak atau Two Tail Test, diperlihatkan pada gambar 2 berikut:
Terdapat beberapa ketentuan dalam penggunaan Uji Dua Pihak yaitu, jika harga t hitung terletak pada daerah penerimaan Ho atau berada diantara nilai tabel, maka Ho diterima dan Ha ditolak, dimana harga t hitung bernilai lebih kecil atau kurang dari sama dengan nilai Ho. Harga t hitung merupakan nilai mutlak yang tidak bernilai postif ataupun juga negatif.
3 2 3 4 5 6 7 8 5 3 4 5 6 6 7 8 8 5 3 4 5 6 2 3 4 5 6 3 2 3 3
Berdasarkan data tersebut, maka
Maka nilai simpangan baku sampel (s) yang dihitung dengan persamaan simpangan baku sampel (s) adalah 1,81.
Maka nilai rata-rata kemampuan berdiri para pelayan toko yang diambil dari 31 data sampel adalah 4,645 jam/hari. Selanjutnya, nilai rata-rata tersebut dilakukan pengujian terhadap tingkat signifikansinya dengan asumsi yang didapat dari keterangan sebelumnya, bahwa daya tahan berdiri pelayan toko adalah 4 jam/hari. Dengan menggunakan rumus 1, maka didapatkan nilai t adalah sebesar 1,98.
Untuk dapat mengambil keputusan dari hasil hipotesis, apakah nilai hipotesis tersebut diterima atau ditolak, maka dapat dilakukan dengan cara membandingkan hasil dari t hitung terhadap t tabel. Nilai t tabel didasarkan pada nilai derajat kebebasan (dk) dengan besaran nilainya adalah n-1, yaitu 31-1=30. Jika toleransi kesalahan (alfa) yang ditetapkan adalah sebesar 5%, dan teknik pengujian yang digunakan adalah uji dua pihak, maka besar harga t tabel adalah 2,042. Secara sederhana, hasil perbandingan antara t hitung dan t tabel diperlihatkan pada gambar 5.3. Berdasarkan gambar tersebut diperlihatkan bahwa nilai t hitung terletak diantara daerah Ho, sehingga hipotesis nol atau Ho diterima. Jika nilai Ho diterima, maka hipotesis yang menyatakan bahwa daya tahan pelayan toko untuk melayani para pelanggan dalam posisi berdiri adalah 4 jam dapat digeneralisasikan terhadap seluruh populasinya seperti diperlihatkan pada gambar 3.
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
One Tail Test Uji pihak kiri diperlihatkan pada gambar 4 berikut:
Pada teknik uji pihak kiri berlaku beberapa ketentuan yaitu, jika nilai t hitung berada pada daerah Ho dan nilainya lebih besar atau sama dengan (≥) dari t tabel, maka Ho diterima dan Ha ditolak.
Untuk langkah pembuktian, selanjutnya dilakuan penelitian dengan data sampel yang diambil dari 25 produk lampu yang diambil secara acak. Kemudian ditemukan data berupa daya tahan lampu sebagai berikut:
450 390 400 480 500 380 350 400 340 300 300 345 375 425 400 425 390 340 350 360 300 200 300 250 400
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
Dengan nilai rata-rata sebesar 366, dan nilai simpangan baku adalah 68,25, selanjutnya dilakukan pengujian menggunakan teknik Uji Pihak Kiri dengan persamaan yang sama seperti pada rumus 1, maka didapatkan nilai t adalah -2,49. Dengan nilai dk adalah 24 (dk=n-1; dk=25-1).
Jadi, nilai t tabel dengan dk adalah 24, maka nilai taraf kesalahan 5% untuk uji satu pihak adalah 1,711. Dari nilai tersebut maka dapat disimpulkan bahwa nilai t hitung jauh pada penerimaan Ha, sehingga Ho ditolak dan Ha diterima. Jadi pernyataan produsen lampu dengan merek Mangkang Sekawan yang menyatakan bahwa daya tahan lampu yang produksi adalah lebih dari 400 jam ditolak. Dan karena nilai Ha diterima, maka dapat dinyatakan bahwa daya tahan lampu yang diproduksi oleh perusahaan lampu dengan merek Mangkah Sekawan adalah lebih kecil dari 400 jam, dengan nilai rata-ratanya adalah 366 jam. Untuk mengetahui posisi kedudukan t hitung terhadap kedudukan t tabel maka dapat diperhatikan melalui gambar 5 berikut ini.
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
Uji pihak kanan diperlihatkan seperti gambar 6 berikut ini:
Pada One Tail Test Uji pihak kanan berlaku beberapa ketentuan yaitu, jika harga t hitung bernilai lebih kecil atau sama dengan (≤) nilai t tabel, maka Ho diterima dan Ha ditolak.
Berdasarkan hipotesis yang telah dibuat peneliti tersebut, selanjutnya dilakukan proses pengumpulan data terhadap 20 pedagang jeruk yang dilakukan secara acak. Dari hasil pengumpulan data terhadap sampel 20 pedagang, maka diperoleh data sebagai berikut:
98 80 120 90 70 100 60 85 95 100 70 95 90 85 75 90 70 90 60 110
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
Dari data sampel yang telah dikumpulkan maka diketahui bahwa nilai penjual rata-rata jeruk per hari adalah 86,65 kg dengan nilai simpangan baku (s) adalah 15,83. Nilai rata-rata dan nilai simpangan baku selanjutnya dimasukkan ke dalam rumus 1, maka didapatkan nilai t adalah 3,77.
Jika ditentukan nilai toleransi kesalahan adalah 5%, maka nilai derajat kesalahan (dk) adalah 19 (karena dk=n-1; dk=20-1; dk=19). Maka nilai t tabel adalah 1,729. Selanjutnya, dilakukan perbadingan nilai antara t hitung terhadap t tabel seperti diperlihatkan pada gambar 7 berikut.
Berdasarkan gambar tersebut, diperlihatkan bahwa nilai t hitung berada pada daerah Ho, sehingga Ho diterima dan Ha ditolak. Jadi dapat disimpulkan bahwa pedagang jeruk setiap hari paling banyak hanya menjual 100 kg adalah bernilai benar.
Tabel 1 Statistik yang Digunakan untuk Menguji Hipotesis Deskriptif Satu Sampel
 | |
|
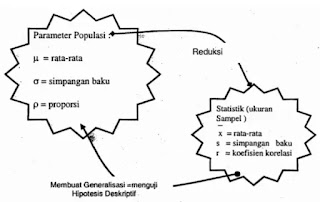
Statistik Parametris pengujian hipotesis deskriptif satu sampel
Statistik parametris adalah jenis statistik yang dapat digunakan dalam proses pengujian hipotesis deskriptif jika jenis data yang digunakan adalah tipe data interval atau tipe data rasio (t-test 1 sampel ). Pada dasarnya terdapat dua persamaan yang dapat digunakan pada pengujian simpangan baku populasi, yaitu rumus t dan rumus z. Rumus z digunakan jika nilai simpangan baku dari populasi telah diketahui, jika tidak maka persamaan yang digunakan adalah persamaan t. Nilai simpangan baku pada sampel dapat diketahui jika data pengamatan telah berhasil terkumpul.Terdapat dua teknik pengujian hipotesis deskriptif dengan menggunakan satu buah sampel, yaitu teknik uji dua pihak atau two tail test dan teknik uji satu pihak atau one tail test. Teknik uji satu pihak juga dibagi lagi menjadi dua jenis yaitu, uji pihak kanan dan uji pihak kiri. Teknik uji mana yang kemudian dapat digunakan pada hipotesis adalah tergantung dari bentuk permasalahan atau pertanyaan yang diajukan dalam kegiatan penelitian.
Baca Juga:
Persamaan yang dapat digunakan dalam proses penghujian hipotesis deskriptif satu sampel yang menggunakan data sampel interval atau rasio diperlihatkan pada rumus 1 berikut.
t = (x̅-μ0)/(s/(√n)) (Rumus 1)
- t adalah nilai t yang dihitung, selanjutnya disebut t hitung
- x̅ adalah rata-rata xi
- µ0 adalah nilai yang dihipotesiskan
- s adalah simpangan baku
- n adalah jumlah anggota sampel
Berikut adalah tahapan yang dilakukan untuk melakukan pengujian hipotesis deskriptif:
- Hitung rata-rata nilai dari data sampel yang diberikan.
- Hitung simpangan baku dari data sampel yang diberikan.
- Hitung nilai atau harga t.
- Hitung nilai atau harga t tabel.
- Terjemahkan hasil yang didapatkan dalam bentuk kurva.
- Posisikan hasil nilai dari t hitung dan t tabel dalam kurva yang telah dibuat.
- Tarik kesimpulan dari hasil pengujian hipotesis yang telah dilakukan.
Uji Dua Pihak atau Two Tail Test
Uji Dua Pihak digunakan jika hipotesis nol (H0) bermakna senilai atau 'sama dengan' dan hipotesis alternatifnya (Ha) bermakna tidak senilai atau 'tidak sama dengan' (Ho =; Ha ≠).Contoh rumusan hipotesis:
- Hipotesis nol: Daya tahan pelayan toko dalam melayani para pelanggan dalam posisi berdiri adalah adalah 8 jam.
- Hipotesis alternatif: Daya tahan pelayan toko dalam melayani para pelanggan dalam posisi berdiri adalah ≠ 8 jam.
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
- Ho: μ = 8 jam
- Ha: μ ≠ 8 jam
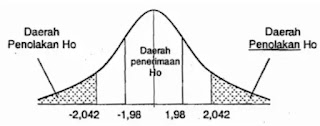
Selanjutnya, Uji Dua Pihak atau Two Tail Test, diperlihatkan pada gambar 2 berikut:
 |
| Gambar 2 Uji Dua Pihak Statistika Penelitian |
Contoh Uji Dua Pihak:
Dilakukan proses pengumpulan data guna menguji hipotesis "daya tahan pelayan toko melayani para pelanggan dalam posisi berdiri di Jakarta adalah 4 jam/hari". Dari data sampel sebanyak 31 individu yang diambil secara acak, didapatkan data bahwa rata-rata para pelayan toko mampu untuk pelayani para pelanggan dalam posisi berdiri adalah sebagai berikut:3 2 3 4 5 6 7 8 5 3 4 5 6 6 7 8 8 5 3 4 5 6 2 3 4 5 6 3 2 3 3
Berdasarkan data tersebut, maka
n = 31
μ0 = 4 jam/hari,
Berapa nilai x̅ dan s?
Nilai x̅ dihitung dengan rumus Σxi/n
x̅ = (3+2+3+...+3+3)/31
x̅ = 144/31
x̅ = 4,645
Maka nilai simpangan baku sampel (s) yang dihitung dengan persamaan simpangan baku sampel (s) adalah 1,81.
Maka nilai rata-rata kemampuan berdiri para pelayan toko yang diambil dari 31 data sampel adalah 4,645 jam/hari. Selanjutnya, nilai rata-rata tersebut dilakukan pengujian terhadap tingkat signifikansinya dengan asumsi yang didapat dari keterangan sebelumnya, bahwa daya tahan berdiri pelayan toko adalah 4 jam/hari. Dengan menggunakan rumus 1, maka didapatkan nilai t adalah sebesar 1,98.
Untuk dapat mengambil keputusan dari hasil hipotesis, apakah nilai hipotesis tersebut diterima atau ditolak, maka dapat dilakukan dengan cara membandingkan hasil dari t hitung terhadap t tabel. Nilai t tabel didasarkan pada nilai derajat kebebasan (dk) dengan besaran nilainya adalah n-1, yaitu 31-1=30. Jika toleransi kesalahan (alfa) yang ditetapkan adalah sebesar 5%, dan teknik pengujian yang digunakan adalah uji dua pihak, maka besar harga t tabel adalah 2,042. Secara sederhana, hasil perbandingan antara t hitung dan t tabel diperlihatkan pada gambar 5.3. Berdasarkan gambar tersebut diperlihatkan bahwa nilai t hitung terletak diantara daerah Ho, sehingga hipotesis nol atau Ho diterima. Jika nilai Ho diterima, maka hipotesis yang menyatakan bahwa daya tahan pelayan toko untuk melayani para pelanggan dalam posisi berdiri adalah 4 jam dapat digeneralisasikan terhadap seluruh populasinya seperti diperlihatkan pada gambar 3.
 |
| Gambar 3 Uji Dua Pihak Statistika Penelitian |
Uji Satu Pihak atau One Tail Test
One Tail Test Uji Pihak Kiri
Uji pihak kiri dapat digunakan jika nilai hipotesis nol atau Ho bermakna "lebih besar atau sama dengan (>=)" dan hipotesis alternatif atau Ha bermakna "lebih kecil atau kurang dari (<)".Contoh rumusan hipotesis:
- Hipotesis nol: Daya tahan lampu merek A adalah minimal 400 jam atau lebih dari sama dengan 400 jam.
- Hipotesis alternatif: Daya tahan lampu merek A adalah kurang dari (<) 400 jam.
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
- Ho : μ ≥ 400 jam
- Ha : μ < 400 jam
One Tail Test Uji pihak kiri diperlihatkan pada gambar 4 berikut:
 |
| Gambar 4 Uji Pihak Kiri Statistika Penelitian |
Pada teknik uji pihak kiri berlaku beberapa ketentuan yaitu, jika nilai t hitung berada pada daerah Ho dan nilainya lebih besar atau sama dengan (≥) dari t tabel, maka Ho diterima dan Ha ditolak.
Contoh Uji Pihak Kiri:
Suatu perusahaan lampu pijar merek Mangkang Sekawan, menyatakan lampu yang diproduksi dari perusahaan tersebut memiliki daya tahan minimal 400 jam. Dari pernyataan produsen tersebut, selanjutnya dilakukan pengujian apakah daya tahan dari lampu yang diprodukti oleh perusahaan tersebut memang lebih dari sama dengan 400 jam atau tidak.Untuk langkah pembuktian, selanjutnya dilakuan penelitian dengan data sampel yang diambil dari 25 produk lampu yang diambil secara acak. Kemudian ditemukan data berupa daya tahan lampu sebagai berikut:
450 390 400 480 500 380 350 400 340 300 300 345 375 425 400 425 390 340 350 360 300 200 300 250 400
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
- Ho : μ ≥ 400 jam
- Ha : μ < 400 jam
Dengan nilai rata-rata sebesar 366, dan nilai simpangan baku adalah 68,25, selanjutnya dilakukan pengujian menggunakan teknik Uji Pihak Kiri dengan persamaan yang sama seperti pada rumus 1, maka didapatkan nilai t adalah -2,49. Dengan nilai dk adalah 24 (dk=n-1; dk=25-1).
Jadi, nilai t tabel dengan dk adalah 24, maka nilai taraf kesalahan 5% untuk uji satu pihak adalah 1,711. Dari nilai tersebut maka dapat disimpulkan bahwa nilai t hitung jauh pada penerimaan Ha, sehingga Ho ditolak dan Ha diterima. Jadi pernyataan produsen lampu dengan merek Mangkang Sekawan yang menyatakan bahwa daya tahan lampu yang produksi adalah lebih dari 400 jam ditolak. Dan karena nilai Ha diterima, maka dapat dinyatakan bahwa daya tahan lampu yang diproduksi oleh perusahaan lampu dengan merek Mangkah Sekawan adalah lebih kecil dari 400 jam, dengan nilai rata-ratanya adalah 366 jam. Untuk mengetahui posisi kedudukan t hitung terhadap kedudukan t tabel maka dapat diperhatikan melalui gambar 5 berikut ini.
 |
| Gambar 5 Uji Pihak Kiri Statistika Penelitian |
One Tail Test Uji Pihak Kanan
One Tail Test Uji pihak kanan dapat digunakan jika hipotesis nol (Ho) bermakna "lebih kecil atau sama dengan (≤)" dan hipotesis alternatifnya (Ha) bermakna "lebih besar atau lebih dari (>)".Contoh rumusan hipotesis:
- Hipotesis nol: Pedagang cilok paling banyak bisa menjual ciloknya sebanyak 100 kg per hari.
- Hipotesis alternatif: Pedagang cilok bisa menjual ciloknya lebih dari 100 kg per hari.
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
- Ho : μ ≤ 100 kg/hari
- Ha : μ > 100 kg/hari
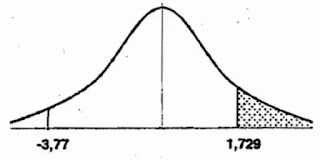
Uji pihak kanan diperlihatkan seperti gambar 6 berikut ini:
 |
| Gambar 6 Uji Pihak Kanan Statistika Penelitian |
Pada One Tail Test Uji pihak kanan berlaku beberapa ketentuan yaitu, jika harga t hitung bernilai lebih kecil atau sama dengan (≤) nilai t tabel, maka Ho diterima dan Ha ditolak.
Contoh Uji Pihak Kanan:
Berdasarkan data pengamatan diperlihatkan bahwa terjadi angka penurunan penjualan buah jeruk, sehingga dilakukan penelitian guna mengetahui besar jumlah jeruk yang dapat terjual (kg) oleh para pedagang pada setiap hari. Dari hasil pengamatan, peneliti kemudian membuat sebuah hipotesis bahwa "pedagang jeruk setiap hari dapat menjual jeruk kepada konsumen paling banyak 100 kg".Berdasarkan hipotesis yang telah dibuat peneliti tersebut, selanjutnya dilakukan proses pengumpulan data terhadap 20 pedagang jeruk yang dilakukan secara acak. Dari hasil pengumpulan data terhadap sampel 20 pedagang, maka diperoleh data sebagai berikut:
98 80 120 90 70 100 60 85 95 100 70 95 90 85 75 90 70 90 60 110
Dari data tersebut selanjutnya dirumuskan dalam bentuk hipotesis:
- Ho : μ ≥ 100 kg/hari
- Ha : μ < 100 kg/hari
Dari data sampel yang telah dikumpulkan maka diketahui bahwa nilai penjual rata-rata jeruk per hari adalah 86,65 kg dengan nilai simpangan baku (s) adalah 15,83. Nilai rata-rata dan nilai simpangan baku selanjutnya dimasukkan ke dalam rumus 1, maka didapatkan nilai t adalah 3,77.
Jika ditentukan nilai toleransi kesalahan adalah 5%, maka nilai derajat kesalahan (dk) adalah 19 (karena dk=n-1; dk=20-1; dk=19). Maka nilai t tabel adalah 1,729. Selanjutnya, dilakukan perbadingan nilai antara t hitung terhadap t tabel seperti diperlihatkan pada gambar 7 berikut.
 |
| Gambar 7 Uji Pihak Kanan Statistika Penelitian |
Referensi Tambahan:
- Pengujian Hipotesis Komparatif Dua Sampel, Sampel Berkorelasi Menggunakan Statistik Nonparametris
- Pengujian Hipotesis Komparatif Dua Sampel, Sampel Independen Menggunakan Statistik Parametris
- Pengujian Hipotesis Komparatif Dua Sampel, Sampel Independen Menggunakan Statistik Nonparametris
- Pengujian Hipotesis Komparatif K Sampel
- Pengujian Hipotesis Komparatif K Sampel, Sampel Berkorelasi Menggunakan Statistik Parametris
- Pengujian Hipotesis Komparatif K Sampel, Sampel Berkorelasi Menggunakan Statistik Nonparametris
- Pengujian Hipotesis Komparatif K Sampel, Sampel Independen Menggunakan Statistik Parametris
Artikel ini didedikasikan kepada: Tasya Aulia Trengga Dewi, Taufik Nabilla, Teresa Puspita Padmadhita, Tiara Dewi, dan Titania Arestanto.
5 komentar untuk "Pengujian Hipotesis Deskriptif Satu Sampel Statistik Parametris"
Hubungi admin melalui Wa : +62-896-2414-6106
Respon komentar 7 x 24 jam, mohon bersabar jika komentar tidak langsung dipublikasi atau mendapatkan balasan secara langsung.
Bantu admin meningkatkan kualitas blog dengan melaporkan berbagai permasalahan seperti typo, link bermasalah, dan lain sebagainya melalui kolom komentar.
- Ikatlah Ilmu dengan Memostingkannya -
- Big things start from small things -
Statistik parametris merupakan cabang ilmu statistik yang mengasumsikan bahwa data sampel berasal dari populasi yang dapat dimodelkan secara memadai oleh distribusi probabilitas yang memiliki sekumpulan nilai parameter tetap.
BalasHapusBagaimana mengatahui teknik uji parametris dan non parametris dapat digunakan pada data penelitian?
BalasHapusJika nilai rata-rata dapat lebih akurat dalam mewakili nilai pusat distribusi data, dan jika ukuran sampel yang digunakan dalam jumlah besar maka dapat digunakan bentuk uji parametris. Namun, jika nilai median lebih akurat dalam mewakili nilai distribusi data, maka dapat digunakan teknik uji nonparametris meskipun jumlah ukuran sampel yang digunakan adalah besar.
HapusTes parametris merupakan tes yang digunakan untuk asumsi mengenai parameter distribusi populasi dimana nilai sampel tersebut diambil.
BalasHapusSelamat hari kebangkitan!!!
BalasHapus