Teknik Sampling Statistika Penelitian dan Penjelasannya

Teknik sampling adalah teknik pengambilan sampel dari sekumpulan data yang besar atau populasi. Untuk dapat menentukan sampel dalam suatu penelitian, terdapat berbagai teknik sampling yang dapat digunakan dalam suatu populasi. Secara skematis, macam-macam teknik sampling diperlihatkan pada gambar 1.

Sebelum mempelajari materi tentang Teknik Sampling Statistika Penelitian dan Penjelasannya, terlebih dahulu pelajari materi tentang: Cara Pengukuran Tendency Central Statistika, Pengukuran Variasi Kelompok Statistika Penelitian, dan Populasi dan Sampel Statistika Penelitian.

Gambar 1 memperlihatkan bahwa Teknik Sampling diklasifikasikan menjadi dua, yaitu probability sampling atau sampel probabilitas dan nonprobability sampling atau sampel non probabilitas. Probability sampling terdiri dari simple random, proportionate satisfied random, disproportionate statified random, dan area random. Nonprobability sampling terdiri dari sampling sistematis, sampling quota, sampling aksidental atau sampling incidental, purposive sampling, sampling jenuh, dan snowball sampling.

Probability Sampling atau sampling probabilitas

Sampling probabilitas merupakan Teknik pengambilan sampling dengan hasil berupa nilai peluang dari setiap unsur atau anggota populasi terpilih sebagai anggota sampel.  Teknik probability sampling terdiri dari simple random sampling, proportionate stratified random sampling, disproportionate stratified random, dan sampling area atau cluster sampling.

Gambar 1 Klasifikasi Teknik Sampling Statistika Penelitian

Simple Random Sampling

Dikatakan simple atau sederhana karena pengambilan anggota sampel dari populasi dilakukan secara acak tanpa memperhatikan strata yang ada dalam populasi yang diteliti. Cara demikian dilakukan bila anggota populasi dianggap homogen. Pengambilan sampel acak sederhana dapat dilakukan dengan cara undian, memilih bilangan dari daftar secara acak, dan lain sebagainya. Perhatikan gambar 2.

Gambar 2 Simple Random Sampling Statistika Penelitian

Proportionate Stratified Random Sampling

Teknik proportionate stratified random sampling digunakan jika populasi memiliki anggota yang tidak homogen secara proporsional. Suatu organisasi profesi terdiri dari pegawai dengan latar belakang Pendidikan yang berstrata, maka populasi organisasi profesi tersebut adalah kelompok dengan Pendidikan berstrata. Misalnya jumlah pegawai yang lulus S1 adalah 45, S2 adalah 30, STM adalah 800, ST adalah 900, SMEA adalah 300, dan lain sebagainya. Jumlah sampel yang harus diambil meliputi strata pendidikan tersebut seperti diperlihatkan pada gambar 3.

Gambar 3 Proportionate Stratified Random Sampling Statistika Penelitian

Disproportionate Stratified Random Sampling

Teknik disproportionate stratified random sampling digunakan pada penentuan jumlah sampel, jika populasi dengan tingkat strata tertentu dinyatakan kurang proporsional. Contoh, pegawai dari suatu divisi memiliki 4 orang lulusan S3, 4 orang lulusan S2, 91 Orang lulusan S1, 801 lulusan SMA dan 701 dari lulusan SMP. Sehingga, 4 orang lulusan S3 dan 5 dari lulusan S2 tersebut diberlakukan sebagai satu sampel, karena nilainya yang terlalu kecil untuk dibandingkan terhadap jumlah lainnya.

Sampling Area atau Cluster Sampling

Teknik Sampling Area atau wilayah digunakan dalam penentuan sampel jika objek yang diteliti cakupannya sangat luas. Contoh, penduduk negara, propinsi, dan kabupaten pada suatu wilayah tertentu. Untuk dapat menentukan kategori penduduk mana yang digunakan sebagai sumber data, maka pengambilan sampling dilakukan dengan proses yang bertahap mulai dari Kawasan wilayah yang paling luas (negara) sampai dengan kawasan wilayah terkecil (kabupaten). Setelah sampel terkecil ditentukan, maka dilakukan pemilihan sampel secara acak.

Contoh, dari seluruh provinsi di Indonesia, diambil 15 provinsi sebagai sampel, dimana proses pengambilan sampel tersebut dilakukan secara acak. Namun, karena provinsi tersebut memiliki berbagai tingkatan atau berstrata, maka pengambilan sampel dilakukan menggunakan stratified random sampling. Kenapa demikian? karena propinsi di Indonesia ada yang pendudukanya padat, ada juga yang tidak, dan ada yang mempunyai banyak hutan namun juga ada juga yang tidak punya banyak hutan, ada yang kaya bahan tambang ada juga yang tidak. Karakteristik tersebut perlu diperhatikan sehingga proses pengambilan sampel berdasarkan populasi berstrata dapat ditetapkan dengan jelas.

Sampling area dapat digunakan pada dua tahap, yaitu pada tahapan penentuan sampel daerah atau wilayah, dan tahap penentuan orang atau individu yang terdapat dalam daerah atau wilayah sampling, seperti digambarkan pada gambar 4 berikut.

Gambar 4 Cluster Sampling Statistika Penelitian

Sampel non probabilitas atau Nonprobability sampling

Teknik sampel ini digunakan pada proses pengambilan sampel yang tidak membutuhkan hasil peluang pada unsur atau anggota populasi yang akan dijadikan sampel. Teknik sampel ini meliputi sampling sistematis, sampling kuota, sampling aksidental, sampling purposive, sampling jenuh, dan sampling snowball.

Sampling Sistematis

Teknik sampling ini digunakan pada proses pengambilan sampel berdasarkan nilai urut dari anggota populasi yang telah diurutkan. Contoh populasi individu pada kumpulan 100 orang. Setelah diberi nomor urut pada tiap individu pada populasi tersebut, proses pengambilan sampel dapat diambil berdasarkan kelipatan urut nomor tertentu, seperti nomor ganjil saja, nomor genap saja, atau kelipatan bilangan prima, dan lain sebagainya. Dari penjelasan tersebut, maka diambil sampel dari nomor 1, 5, 10, 15, 20, dan seterusnya hingga nomor 100, seperti diperlihatkan pada gambar 5.

Gambar 5 Sampling Sistematis Statistika Penelitian

Sampling Kuota

Teknik sampling kuota digunakan pada penentuan sampel dalam populasi yang memiliki ciri-ciri tertentu hingga jumlah kuota dengan ciri tersebut terpenuhi. Contoh, dilakukan penelitian tentang pendapat masyarakat terhadap pelayanan masyarakat dalam urusan Ijin Mendirikan Bangunan (IMB). Jumlah sampel yang ditentukan adalah 500 orang. Jika pengumpulan data belum memenuhi kuota 500 orang, maka penelitian akan dianggap belum selesai. Dan jika proses pengambilan sampel dilakukan berkelompok yang terdiri dari 5 anggota kelompok, maka setiap anggota kelompok tersebut harus dapat menghubungi 100 anggota lainnya dalam anggota sampel.

Baca Juga:

• Pengujian Hipotesis Statistika Penelitian dan Penjelasannya
• Rumusan Hipotesis Statistika dan Penjelasannya
• Tingkat Kesalahan Pengujian Hipotesis Statistika Penelitian
• Kesalahan Pengujian Hipotesis Statistika Penelitian

Sampling Incidental

Sampling incidental merupakan Teknik sampling yang digunakan pada penentuan penarikan sampel berdasarkan faktor kebetulan. Contoh, individu mana saja yang secara secara kebetulan ditemui oleh peneliti pada kegiatan penelitiannya dapat digunakan sebagai sampel, dengan catatan orang yang ditemui secara kebetulan tersebut cocok dengan sumber data yang dibutuhkan.

Sampling Purposive

Sampling ini merupakan salah satu Teknik sampling yang diambil berdasarkan kondisi pertimbangan tertentu. Contoh, dilakukan penelitian terkait kualitas makanan, maka sampel yang diambil adalah para pakar dibidang kuliner, atau contoh lain seperti penelitian terkait dengan kondisi perpolitikan suatu daerah tertentu, maka sampel yang diambil adalah para pakar politik. Teknik sampling ini kebanyakan digunakan pada metode penelitian kualitatif atau jenis penelitian yang tidak membutuhkan generalisasi terhadap hasil penelitiannya.

Sampling Jenuh

Merupakan Teknik sampling yang diambil jika semua anggota populasi dapat digunakan sebagai sampel. Kondisi ini sering terjadi jika jumlah populasi yang akan dijadikan sampel adalah relatif kecil, atau proses penelitian dengan hasil generalisasi yang ingin diambil adalah sangat kecil. Istilah lain dari sampling jenuh adalah sensus.

Snowball Sampling

Teknik ini merupakan Teknik pengambilan sampel yang awalnya berukuran kecil, kemudian perlahan dan bertahap menjadi membesar. Teknik snowball sampling dapat juga diibaratkan bola salju yang menggelinding yang lama kelamaan akan menjadi besar. Pada Teknik ini proses pengambilan sampel dimulai dengan cara pemilihan satu atau dua individu, tetapi setelah dilakukan penelitian ternyata sampel awal yang diambil tersebut ternyata belum lengkap, atau belum bisa memberikan data yang dibutuhkan dalam penelitian, sehingga peneliti kemudian menambah lagi sampel lain yang dianggap bisa melengkapi data, dan seterusnya hingga data ideal didapatkan. Pada gambar 6 diperlihatkan Teknik pengambilan sampling snowball yang menggunakan penelitian kualitatif. Contoh, kegiatan penelitian untuk meneliti siapa yang menjadi provokator pada kegiatan unjuk rasa, atau dalang dalam kegiatan teroris pada wilayah tertentu.

Gambar 6 Snowball Sampling Statistika Penelitian

Jumlah anggota pada suatu populasi dinyatakan dalam ukuran sampel, maka sampel yang mewakili 100% populasi adalah sama dengan jumlah anggota populasi itu sendiri. Jadi, jika populasi berjumlah 1000 sampel, dan hasil penelitian tersebut diberlakukan terhadap 1000 anggota populasi itu sendiri tanpa ada kesalahan, maka jumlah sampel yang diambil adalah sama dengan jumlah dari populasi itu sendiri sebesar 1000. Semakin besar jumlah sampel yang diambil, yang jumlahnya mendekati jumlah populasi keseluruhan, maka peluang kesalahan dari generalisasinya adalah semakin kecil dan begitupun sebaliknya.

Berapa jumlah ideal pengambilan sampel pada kegiatan penelitian? Jawabannya adalah tergantung dari tingkat ketelitian yang dikehendaki oleh peneliti pada kegiatan penelitian. Tingkat ketelitian bergantung pada sumber daya penelitian seperti biaya, waktu pelaksanaan, dan tenaga yang dibutuhkan pada kegiatan penelitian.

Berikut tabel 1 diperlihatkan penentuan terhadap jumlah sampel dari populasi yang dikembangkan berdasarkan persamaan Krejcie dan Morgan (1970) dengan tingkat kesalahan adalah 1%, 5%, dan 10%. Dengan rumus perhitungan diperlihatkan sebagai berikut.

Tabel 1 Krejcie dan Morgan

N	Siginifikasi			N	Siginifikasi			N	Siginifikasi
	1%	5%	10%		1%	5%	10%		1%	5%	10%
10	10	10	10	280	197	155	138	2800	537	310	247
15	15	14	14	290	202	158	140	3000	543	312	248
20	19	19	19	300	207	161	143	3500	558	317	251
25	24	23	23	320	216	167	147	4000	569	320	254
30	29	28	28	340	225	172	151	4500	578	323	255
35	33	32	32	360	234	177	155	5000	586	326	257
40	38	36	36	380	242	182	158	6000	598	329	259
45	42	40	39	400	250	186	162	7000	606	332	261
50	47	44	42	420	257	191	165	8000	613	334	263
55	51	48	46	440	265	195	168	9000	618	335	263
60	55	51	49	460	272	198	171	10000	622	336	263
65	59	55	53	480	279	202	173	15000	635	340	266
70	63	58	56	500	285	205	176	20000	642	342	267
75	67	62	59	550	301	213	182	30000	649	344	268
80	71	65	62	600	315	221	187	40000	563	345	269
85	75	68	65	650	329	227	191	50000	655	346	269
90	79	72	68	700	341	233	195	75000	658	346	270
95	83	75	71	750	352	238	199	100000	659	347	270
100	87	78	73	800	363	243	202	150000	661	347	270
110	94	84	78	850	373	247	205	200000	661	347	270
120	102	89	83	900	382	251	208	250000	662	348	270
130	109	95	88	950	391	255	211	300000	662	348	270
140	116	100	92	1000	399	258	213	350000	662	348	270
150	122	105	97	1100	414	265	217	400000	662	348	270
160	129	110	101	1200	427	270	221	450000	663	348	270
170	135	114	105	1300	440	275	224	500000	663	348	270
180	142	119	108	1400	450	279	227	550000	663	348	270
190	148	123	112	1500	460	283	229	600000	663	348	270
200	154	127	115	1600	469	286	232	650000	663	348	270
210	160	131	118	1700	477	289	234	700000	663	348	270
220	165	135	122	1800	485	292	235	750000	663	348	270
230	171	139	125	1900	492	294	237	800000	663	348	271
240	176	142	127	2000	498	297	238	850000	663	348	271
250	182	146	130	2200	510	301	241	900000	663	348	271
260	187	149	133	2400	520	304	243	950000	663	348	271
270	192	152	135	2600	529	307	245	1000000	663	348	271
								∞	664	349	272

catatan: Beberapa sumber literatur ada yang mengatakan bahwa persamaan penentuan ukuran sample adalah persamaan yang dikembangkan oleh Isaac dan Michael, namun informasi tersebut tidak ditemukan pada sumber arsip yang dicari penulis, melainkan formula atau rumus yang dikembangkan oleh Krejcie dan Morgan pada tahun 1970 dalam jurnal yang "Determining Sample Size for Research Activities...]". Artikel penentuan ukuran sample PDF...]

s = (X²NP(1-P))/(d²N-1)+X²P(1-P))       (Rumus 1)

• s adalah Jumlah Sample
• X² adalah nilai tabel chi-square untuk 1 derajat kebebasan pada tingkat kepercayaan yang diinginkan (3,841)
• N adalah Jumlah Populasi
• P adalah Proporsi populasi (diasumsikan 0,5 karena ini akan memberikan ukuran sampel maksimum)
• d adalah tingkat akurasi yang dinyatakan sebagai proporsi (0,05)

Berdasarkan rumus 1 didapatkan hasil perhitungan sampel dari populasi mulai 10 sampai dengan 1.000.000. Dari tabel 1. diperlihatkan bahwa, makin besar taraf kesalahan, maka akan semakin kecil ukuran sampel. Contoh, untuk populasi 1000, dengan taraf kesalahan 1%, jumlah sampelnya adalah 399. Untuk taraf kesalahan 55 jumlah sampelnya adalah 258, dan untuk taraf kesalahan 10%, jumlah sampelnya adalah 213. Dari tabel juga terlihat bahwa bila jumlah populasi tak terhingga, maka jumlah anggota sampel untuk kesalahan 1% sama dengan 664,55 adalah 349, dan 10% adalah 272. Untuk jumlah populasi 10 jumlah anggota sampel sebenernya hanya 9,56 tetapi dilakukan pembulatan sehingga menjadi 10.

Cara menentukan ukuran sampel seperti dikemukakan sebelumnya adalah berdasarkan asumsi bahwa populasi terdistribusi normal. Bila sampel tidak terdistribusi normal, misalnya populasi homogen maka cara-cara tersebut tidak perlu dipergunakan. Misalnya populasi benda, katakanlah benda tersebut adalah logam yang susunan molekulnya homogen, maka jumlah sampel yang diperlukan 1% saja sudah bisa mewakili secara keseluruhan.

Terdapat berbagai rumus untuk menghitung ukuran sampel, misalnya dari Cochran, Cohen, dan lain sebagainya. Bila rumus tersebut digunakan pada perhitungan ukuran sampel, maka hasilnya akan menunjukkan sedikit perbedaan jumlah. Jika demikian, maka rumus maka yang sebaiknya dipergunakan para proses perhitungan? untuk dapat menentukan hal tersebut maka yang dipakai adalah jumlah ukuran sampel yang paling besar.

Selanjutnya pada gambar 7 berikut ini diberikan cara menentukan jumlah anggota sampel dengan menggunakan Nomogram Harry King...]

Gambar 7 Nomogram Harry King Statistika Penelitian

Dalam Nomogram Herry King, jumlah populasi maksimum adalah 2000, dengan taraf kesalahan yang bervariasi, mulai dari 0,3% sampai dengan 15%, dan faktor pengali yang disesuaikan dengan taraf kesalahan yang ditentukan. Dalam nomogram tersebut juga, diperlihatkan bahwa interval kepercayaan sebesar 80% dengan faktor pengalinya adalah sebesar 0,780, sedangkan untuk 85% faktor pengalinya adalah sebesar 0,785, untuk 99% faktor pengalinya adalah sebesar 1,195, dan terakhir untuk 99% faktor pengalinya adalah sebesar 1,573.

Contoh: Jumlah populasi adalah sebesar 200. Jika tingkat kepercayaan yang diinginkan terhadap populasi tersebut adalah sebesar 95%, maka sampel yang diambil adalah sebanyak 0,58 x 200 x 1,195 = 19,12 atau dibulatkan menjadi 19 orang. (Tarik dari angka 200 melewati taraf kesalahan 5%, maka akan ditentukan titik diatas angka 60. Titik tersbut berkisar antara nilai 58, untuk kesalahan sebesar 5% berarti tingkat kepercayaannya adalah sebesar 95%, dengan faktor pengali adalah 1,195.

Contoh Teknik Penentuan Ukuran Sampel

Akan dilakukan penelitian untuk mengetahui tanggapan kelompok masyarakat terhadap pelayanan yang diberikan oleh Pemerintah Daerah tertentu. Kelompok masyarakat tersebut terdiri dari 1000 orang, yang dapat dikelompokkan berdasarkan jenjang pendidikan, yaitu lulusan S1 adalah 50, Sarjana Muda adalah 300, SMK adalah 500, SMP adalah 100, dan SD adalah 50.

Berdasarkan tabel 1, jika populasi berjumlah 1000, dengan tingkat kesalahan sebesar 5%, maka jumlah sampel adalah 258. Karena populasi tersebut berstrata atau memiliki tingkatan, maka sampel yang diambilpun juga memiliki strata, yang diambil berdasarkan jenjang Pendidikan pada populasi. Jadi, proses pengambilan sampel proporsionalnya berdasarkan tingkat pendidikan pada populasi. Dari hasil pengambilan sampel tersebut, kemudian didapat data bahwa tingkat pendidikan dari strata S1 adalah sebanyak 13 individu, Sarjana Muda adalah sebanyak 77 individu, SMK adalah sebanyak 129 individu, dan SMP adalah sebanyak 26 individu, dan terakhir SD adalah sebanyak 13 individu.

S1 = 50/1000 X 258
S1 = 12,9
S1 = 13

SM = 300/1000 X 258
SM = 77,4
SM = 78

SMK = 500/1000 X 258
SMK = 129

SMP = 100/1000 X 258
SMP = 25,8
SMP = 26

SD = 50/1000 X 258
SD = 12,9
SD = 13

Jumlah, 
12,9 + 77,4 + 129 + 25,8 + 12,9 = 258

Dengan hasil pecahan yang dibulatkan, maka sampel yang didapat adalah:
13 + 78 + 129 + 26 + 13 = 258

Dari perhitungan yang menghasilkan nilai pecahan, selanjutnya dilakukan pembulatan nilai ke atas, sehingga jumlah sampel bernilai lebih dari 259, nilai ini lebih aman ketimbang hasil yang bernilai kurang dari 259. Gambaran jumlah populasi dan sampel tersebut dapat ditunjukkan lebih jelas pada gambar 8 berikut ini:

Gambar 8 Populasi dan Sample Statistika Penelitian

Roscoe dalam buku Research Mothods For Business (1982:253) memberikan beberapa saran tentang ukuran sampel untuk penelitian, yakni sebagai berikut:

• Ukuran sampel bernilai layak pada kegiatan penelitian adalah sebesar 30 sampai dengan 500.
• Jika sampling dibagi ke dalam kategori tertentu, maka jumlah anggota sampel pada tiap-tiap kriteria adalah minimal sebesar 30.
• Jika pada penelitian dilakukan analisis dengan multivariabel baik itu menggunakan analisis korelasi atau regresi ganda, maka jumlah sampel adalah minimal sebesar 10x dari jumlah variabel yang akan diteliti. Contoh, variabel penelitian sebesar 5 yang terdiri dari variabel independen dan dependen, maka jumlah sampel adalah sebesar 10 x 5 = 50.
• Pada kegiatan penelitian sederhana menggunakan kelompok eksperimen dan kelompok kontrol, maka jumlah dari sampel masing-masing kelompok berkisar 10 sampai dengan 20.  

Cara Pengambilan Anggota Sampel

Pada teknik pengambilan sampel terdapat dua bua teknik untuk melakukan sampling, yaitu probability sampling dan non probability sampling. Pengambilan sampel probabilitas atau probability sampling memberikan peluang bernilai sama terhadap anggota populasi untuk menjadi bagian dari sampel tersebut, cara ini sering disebut dengan Teknik sampling acak (random). Proses pengambilan sampel acak dapat dilakukan menggunakan bilangan random menggunakan komputer ataupun media lainnya. Jika pengambilan dilakukan dengan cara undian atau acak, maka anggota populasi yang akan diundi diberi nomor terlebih dahulu sesuai dengan jumlah populasi.

Karena sifatnya yang acak, maka setiap anggota pada populasi memiliki peluang sama untuk mejadi sampel penelitian. Untuk contoh tersebut maka peluang setiap anggota populasi adalah 1:1000. Jadi, bila salah satu nomor telah diambil, maka harus dikembalikan lagi, jika tidak dikembalikan maka peluangnya menjadi tidak sama lagi. Misalnya, nomor pertama tidak dikembalikan lagi, maka peluang berikutnya adalah menjadi 1:999. Peluang akan semakin besar jika anggota yang telah diambil tidak dikembalikan lagi ke dalam populasi. Jika peluang yang telah diambil muncul lagi maka dianggap tidak sah dan dikembalikan lagi ke dalam populasi.

Kurva Normal pada Normalitas Data

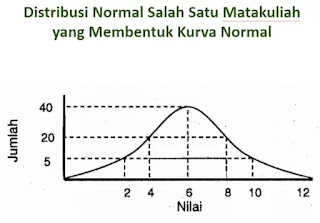
Statistik Parametrik digunakan dengan asumsi bahwa setiap variabel data yang dianalisis akan membentuk pola distribusi normal. Jika data tidak bernilai normal, maka teknik ini tidak bisa digunakan pada kegiatan penelitian. Sebagai gantinya dari teknik tersebut, maka digunakan teknik statistik lain yang tidak memerlukan asumsi data dalam bentuk distribusi normal atau menggunakan statistik non parametris. Sebelum peneliti menggunakan teknik statistik parametris sebagai analisisnya, maka peneliti harus membuktikan terlebih dahulu apakah data yang digunakan tersebut terdistribusi normal atua tidak.

Suatu data yang membentuk distribusi normal bila jumlah rata-rata data atas dan bawahnya adalah sama, demikian juga simpangan bakunya, seperti diperlihatkan pada gambar 9.

Gambar 9 Kurva Normal Statistika Penelitian

Dari gambar 9 diperlihatkan bahwa nilai rata-rata 190 mahasiswa adalah 6,5. Jumlah mahasiswa adalah sama yaitu 40 + 20 + 5 = 65. Demikian juga dengan nilai simpangan bawah dan atas dari nilai rata-rata adalah sama, yaitu 30. Dari gambar 9 diperlihatkan bahwa kurva normal terjadi setelah persilangan antara titik pertemuan antar nilai, terhadap frekuensi yang dihubungkan.

Kurva normal dibagi berdasarkan jumlah standar deviasi pada kelompok data yang membentuk distribusi normal. Luas antara rata-rata (mean) terhadap satu standar deviasi (SD) ke kiri dan ke kanan masing-masing adalah 34,13%; luas antara standar deviasi ke satu (1 SD) ke dua (2 SD) masing-masing adalah 13,59%, dan luas standar deviasi ke dua (2 SD) sampai standar deviasi ke tiga (3 SD) masing-masing adalah 2,27% seperti diperlihatkan pada gambar 10. Jumlah standar deviasi dari satu kelompok tidak terhingga, oleh karena itu secara teor kurva normal tidak akan pernah menyentuh garis dasar, sehingga luasnyapun tidak sampai 100% tetapi hanya mendekati 100%.

Gambar 10.a Luas Kurva Normal Statistika Penelitian

Gambar 10.b Luas Kurva Normal Statistika Penelitian

Kurva normal yang telah dibahas sebelumnya adalah kurva normal umum. Nilai rata-rata (mean) dan simpangan baku (1s, 2s, 3s, dan seterusnya) yang ada kurva normal tergantung pada nilai yang ada dalam kelompok yang telah diperoleh melalui proses pengumpulan data. Kurva berbentuk sistematis, sehingga nilai rata-rata luas (mean) ke kanan dan ke kiri mendekati nilai 50%. Selain terdapat kurva normal umum, juga terdapat kurva normal yang lain yang disebut juga kurva standar. Dikatakan standar, karena nilai rata-ratanya adalah 0 dan simpangan bakunya adalah 1, 2, 3, 4, dan seterusnya. Nilai simpangan baku selanjutnya dinyatakan dalam simbol z. Kurva normal umum dapat dirubah ke dalam kurva normal standar, dengan menggunakan rumus 2.

z = (Xi-x̅)/s               (Rumus 2)

• z adalah Simpangan Baku untuk Kurva Normal Standar
• Xi adalah Data ke i dari suatu kelompok data
• x̅ adalah Rata-rata Kelompok
• s adalah Simpangan Baku

Harga-harga z ada kaitannya dengan nilai persentase daerah kurva. Persentase daerah kurva dihitung berdasarkan nilai dari rata-rata atau mean. Dalam hal ini nilai rata-ratanya adalah 0. Misal, nilai z adalah 1,0, maka luas kurva dari 0 sampai 1 adalah 34,13% seperti diperlihatkan pada gambar 10.

Contoh Penggunaan Kurva Normal

Ada 200 mahasiswa yang akan mengikuti kegiatan ujian mata kuliah statistik. Nilai dari 200 mahasiswa tersebut adalah sebesar 6 dengan nilai simpangan bakunya adalah sebesar 2. Berapa orang yang mendapat nilai 8 ke atas?

Jawab: 
Rata-rata kelas (x) = adalah 6, dan simpangan baku (s) =2. Dari rumus 2 maka nilai dari z dapat dihitung sebgai berikut.
z = (xi-x_)/s
z = (8-6)/2
z = 1

Dari tabel kurva normal dapat dilihat bahwa daerah 0 sampai dengan 1, luasnya adalah 34,13. Nilai ini merupakan jarak mean atau rata-rata dengan titik yang jauhnya 1 SD diatas nilai rata-rata. Harga ini menunjukkan persentase jumlah mahasiswa yang mendapat nilai antara 6 sampai dengan 8. Dengan demikian persentase yang mendapat nilai lebih dari 8 adalah 50% - 34,13% = 15,87% (50% adalah setengah kurva di atas mean, dimana posisi nilai 8 ke atas berada). Jadi mahasiswa yang mendapat nilai 8 ke atas adalah 15,87% X 200 = 31,74 orang atau sekitar 32 orang seperti diperlihatkan pada gambar 11.

Gambar 11 Penggunaan Kurva Normal Statistika Penelitian

• Menentukan jumlah kelas interval. Untuk pengujian normalitas dengan Chi Kuadrat, jumlah kelas interval ditetapkan adalah 6. Hal ini bersesuaian dengan 6 bidang yang terdapat pada kurva baku normal.
• Pengujian Normalitas Data: Statistik parametris bekerja dengan asumsi jika data setiap variabel yang akan dianalisis adalah berupa distribusi normal. Sebelum seorang peneliti menggunakan Teknik statistik parametris, terlebih dahulu dilakukan pengujian kenormalan data yang akan digunakan pada kegiatan penelitian. Jika data yang digunakan tidak normal, maka Teknik statistik ini tidak dapat digunakan atau menggunakan Teknik lain yaitu statistik non parametris. Tetapi perlu perlu diketahui juga apa yang menyebabkan suatu data menjadi tidak normal? Contoh, jika pada kegiatan penelitian terjadi kesalahan pemilihan instrumen dan proses pengumpulan data, maka hal ini akan mengakibatkan data menjadi tidak normal. Namun, jika sekelompok data yang dikumpulkan tersebut bernilai tidak valid, dan distribusinya tidak membentuk distribusi normal, maka peneliti dapat mengambil keputusan untuk menggunakan statistik non parametris.
• Contoh, diberikan suatu teknik pengujian normalitas data menggunakan persamaan Chi Kuadrat. Pengujian normalitas data tersebut dilakukan dengan cara melakukan perbandingan kurva normal pada data terhadap kurva nomal baku. Jika nilai B tidak berbeda secara signifikan dengan A, maka B merupakan data yang terdistribusi normal.
• Pada gambar 10, diperlihatkan bahwa kurva baku normal memiliki luas yang mendekati 100% dan dibagi menjadi 6 bidang, berdasarkan simpangan baku dari kurva tersebut, yang berupa tiga bidang beraada di bawah nilai rata-rata dan tiga lainnya berada di atas nilai rata-rata. Luas ke 6 bidang kurva normal baku tersebut adalah sebagai berikut 2,27%; 13,53%; 34,13%; 34,13%; 13,53%; 2,27%
• Contoh: Data nilai ujian Mata Kuliah Statistik 150 mahasiswa, setelah diuji dengan kertas peluang normal, maka selanjutnya akan diuji normalitasnya dengan menggunakan persamaan Chi Kuadrat (χ²).
• Menentukan panjang kelas interval.
• Panjang kelas = (Data terbesar-data terkecil)/Jumlah kelas interval
• PK = (94-13)/6
• PK = 13,5 dibulatkan menjadi 14
• Proses penyusunan ke dalam tabel distribusi frekuensi yang merupakan tabel penolong dalam perhitungan nilai hitung Chi Kuadrat, seperti diperlihatkan pada tabel 2.

Tabel 2 Chi Kuadrat

Interval Nilai	f0	fh	f0 - fh	(f0 - fh)²	((f0 - fh)²)/fh
13 - 27	3	4	-1	1	0,25
28 - 42	21	20	1	1	0,05
43 - 57	56	51	5	25	0,49
58 - 72	45	51	-6	36	0,70
73 - 87	21	20	1	1	0,05
88 - 102	4	4	0	0	0
Jumlah	150	150	0	-	1,55

• catatan: f0 adalah frekuensi atau jumlah data hasil observasi, fh adalah jumlah atau frekuensi yang diharapkan dengan persentase luas tiap bidang dikalikan dengan n, dan f0-fh adalah selisih data f0 dengan fh.
• Menghitung fh (frekuensi yang diharapkan)
• Nilai fh dihitung berdasarkan pada nilai persen luas tiap bidang kurva normal yang dikalikan jumlah data observasi. Dalam hal ini jumlah individu dalam sampel adalah 150. Jadi:
• Baris pertama dari atas, 2,7% x 150 = 4,05 dibulatkan menjadi 4
• Baris ke dua, 13,53% x 150 = 20,30 dibulatkan menjadi 20
• Baris ke tiga, 34,13% x 150 = 51,20 dibulatkan menjadi 51
• Baris ke empat, 34,13% x 150 = 51,20 dibulatkan menjadi 51
• Baris ke lima, 13,53% x 150 = 20,30 dibulatkan menjadi 20
• Baris ke enam, 2,7% x 150 = 4,05 dibulatkan menjadi 4
• Masukkan nilai fk pada tabel fh, untuk mendapatkan nilai Chi Kuadrat. 
• Membandingkan harga Chi Kuadrat Hitung dengan Chi Kuadrat Tabel. Jika nilai Chi kuadrat hitung lebih kecil daripada nilai Tabelnya, maka distribusi bernilai normal, dan juga sebaliknya.
• Kesimpulan, dalam proses perhitungan, ditemukan bahwa nilai Chi Kuadrat hitung adalah 1,55. Kemudian, nilai tersebut dibandingkan dengan nilai Chi Kuadrat tabel dengan dk (derajat kesebelas) 6-1 = 5. Berdasarkan Tabel Distribusi Chi Kuadrat...] (PDF), dapat diketahui bahwa nilai dk adalah 5, dan batas toleransi kesalahan yang ditetapkan adalah 5%, maka harga Chi Kuadrat tabel adalah 11,070. Karena harga Chi Kuadrat Hitung (1,55) lebih kecil dari harga Chi Kuadrat Tabel (11,070), maka distribusi data nilai statistik 150 mahasiswa tersebut dapat dinyatakan berdistribusi normal.

Referensi Tambahan:

• Pengujian Hipotesis Deskriptif Satu Sampel Statistik Parametris
• Pengujian Hipotesis Deskriptif Satu Sampel Statistik Nonparametris
• Pengujian Hipotesis Komparatif Statistika
• Pengujian Hipotesis Komparatif Dua Sampel
• Pengujian Hipotesis Komparatif Dua Sampel, Sampel Berkorelasi Menggunakan Statistik Parametris
• Pengujian Hipotesis Komparatif Dua Sampel, Sampel Berkorelasi Menggunakan Statistik Nonparametris
• Pengujian Hipotesis Komparatif Dua Sampel, Sampel Independen Menggunakan Statistik Parametris

Artikel ini didedikasikan kepada: Siti Muamanah, Syarif Kavi Muhammad, Synthia Dewi Nurul Imaniah, Talitha Sari Ismaniar, dan Tasya Ardilla Pramesthi.

Location: Semarang, Kota Semarang, Jawa Tengah, Indonesia

Berbagi :